The OpenGL code used to generate these images lives in this github project.

When working with Catmull-Clark subdivision surfaces in the absence of tessellation shaders, we typically perform some sort of uniform refinement on the CPU, perhaps using OpenSubdiv.

One of the nice properties of Catmull-Clark is that you always get a clean quad mesh after one level of subdivision, even though the input topology can be composed of arbitrary polygons.

Subdivision surfaces aren’t the only source of quad meshes nowadays; they can also crop up with terrain rendering and visualization of parametric functions.

Vertex Submission for Quad Meshes

Ideally, you could send an indexed quad mesh to OpenGL, but QUADS aren’t in Modern OpenGL. You could use indexed TRIANGLES, but that’s less than ideal because of the repeated indices.

Fret not, it’s easy enough to emulate indexed QUADS using LINES_ADJACENCY, chosen solely because its primitive size is 4 verts. You can draw the quad mesh from C like this:

glDrawElements(GL_LINES_ADJACENCY, numQuads * 4, GL_UNSIGNED_SHORT, 0);

To make this work, use a geometry shader that generates a small triangle strip for every four vertices, like so:

uniform mat4 ObjectToClip;
in vec4 vPosition[4];

layout(lines_adjacency) in;
layout(triangle_strip, max_vertices = 4) out;

void emit(int index)
{
    gl_Position = ObjectToClip * vPosition[index];
    EmitVertex(); 
}

void main()
{
    emit(0); emit(1); emit(3); emit(2);
    EndPrimitive();
}

While you’re at it, you can also compute facet normals in the geometry shader:

out vec3 gNormal;
...
void main()
{
    vec3 A = vPosition[0].xyz;
    vec3 B = vPosition[1].xyz;
    vec3 C = vPosition[2].xyz;
    gNormal = InverseTranspose * normalize(cross(B - A, C - A));
    ...
}

Computing Smooth Normals on the GPU

If the faceted look isn’t what you need, computing smooth normals is also possible in OpenGL with a little more work. In the first pass, compute facet normals in the geometry shader and dump them into a transform feedback buffer:

glEnable(GL_RASTERIZER_DISCARD);
glBindBufferBase(GL_TRANSFORM_FEEDBACK_BUFFER, 0, buffers.facetNormals);
glBeginTransformFeedback(GL_POINTS);
//...draw quads here...
glEndTransformFeedback();
glDisable(GL_RASTERIZER_DISCARD);

For the second pass, bind the facet normals as a texture buffer, along with a vertex-to-face lookup table:

glActiveTexture(GL_TEXTURE1);
glBindTexture(GL_TEXTURE_BUFFER, textures.vertexToFace);
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_BUFFER, textures.facetNormals);

The vertex-to-face lookup table is easy to build on the CPU; it’s just the inverse of the usual index buffer. The vertex shader in your second pass can use the vertexToFace mapping to find adjoining faces and sum up their facet normals:

uniform samplerBuffer FacetNormals;
uniform usamplerBuffer VertexToFace;

void main()
{
    vCrease = 0;
    uvec4 faces = texelFetch(VertexToFace, int(gl_VertexID));
    vec3 n = vec3(0);
    for (int c = 0; c < 4; c++) {
        if (faces[c] != 0xffffu) {
            int quad = int(faces[c]);
            vec3 facetNormal = texelFetch(FacetNormals, quad).xyz;
            n += facetNormal;
        }
    }
    n = normalize(n);
    ...

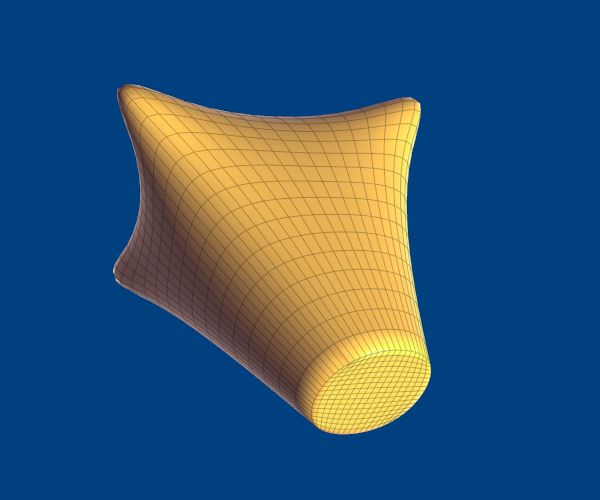
Note that naive smoothing like this can result in undesirable lighting near sharp creases:

This could be improved by creating a buffer with sharpness information, similar to the sharpness tags that you can give to OpenSubdiv. The vertex shader could use this give weights to the adjacent facets.

Disclaimer

Keep in mind that tessellation shaders are the way to go if you’re being truly modern, in which case most of this article is moot. Moreover, Pixar’s OpenSubdiv library provides tessellation shaders for you. However, if you need to support older platforms (e.g., Apple’s current OpenGL implementation) then you might want to consider the techniques discussed in this article. Check out my github repo for a code sample, which builds on OS X and Linux.

Also be aware that some GPUs don’t handle geometry shaders very well, and that they can be detrimental to performance. You might be better off with indexed triangles or triangle strips in these cases, despite the annoying repetition of indices.