Perfect Panning

This is a quick note about through the lens camera control. The user drags the mouse around in their viewport, which causes the camera to slide around within the plane that is parallel to the near and far clipping planes.

This is super easy to implement, but it’s somewhat tricky if you want the user to feel like they’re grabbing something in the scene – especially if you consider the distortion caused by perspective projection.

For example, the following screenshots show a terrain that has been dragged towards the southwest. Since the mountain top appears to move faster than the coastline, how do you make the 3D scene “stick” to the mouse cursor?

To solve this problem the right way, it helps to leverage a raycaster, even if your actual rendering is done with OpenGL. I also find it helpful to pretend that the mouse cursor lives within the near or far planes of the viewing frustum.

So, if you cast a ray from the camera’s position to the cursor’s position, you’ll hit the point in the scene that needs to be stable during the pan. In the following diagram, we’ve panned the camera from A to B such that point C has remained stable. The cursor at the start of the pan was projected onto the far plane at E, and the cursor’s current position corresponds to point D.

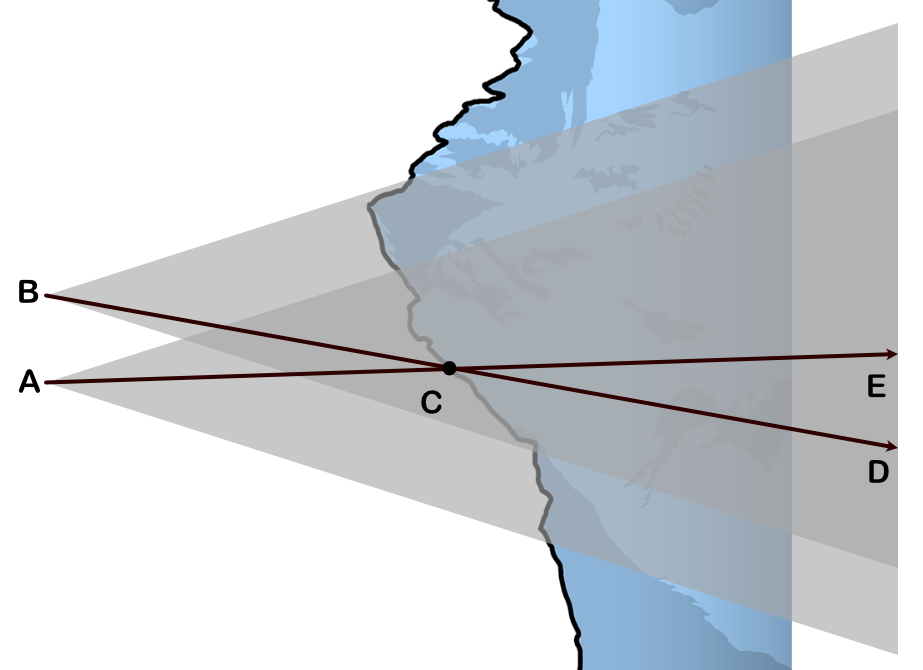
We wish to solve for B, given that A, C, and E are known quantities, assuming that your game engine can perform basic raycasts.

What’s less obvious is that D is also a known quantity (sort of). At any point in time during the drag, you can project the current mouse position onto the current far plane and get D. If you stash A, C, E at the start of the pan and never forget them, then you won’t accumulate error while the user pans.

The next thing to notice is that ΔCAB is similar to ΔCED. Applying the law of similar triangles yields:

|A-B| / |A-C| == |E-D| / |E-C|

This allows you to solve for |A-B|:

|A-B| = |A-C| * |E-D| / |E-C|

Thus, we have a “perfect panning” algorithm:

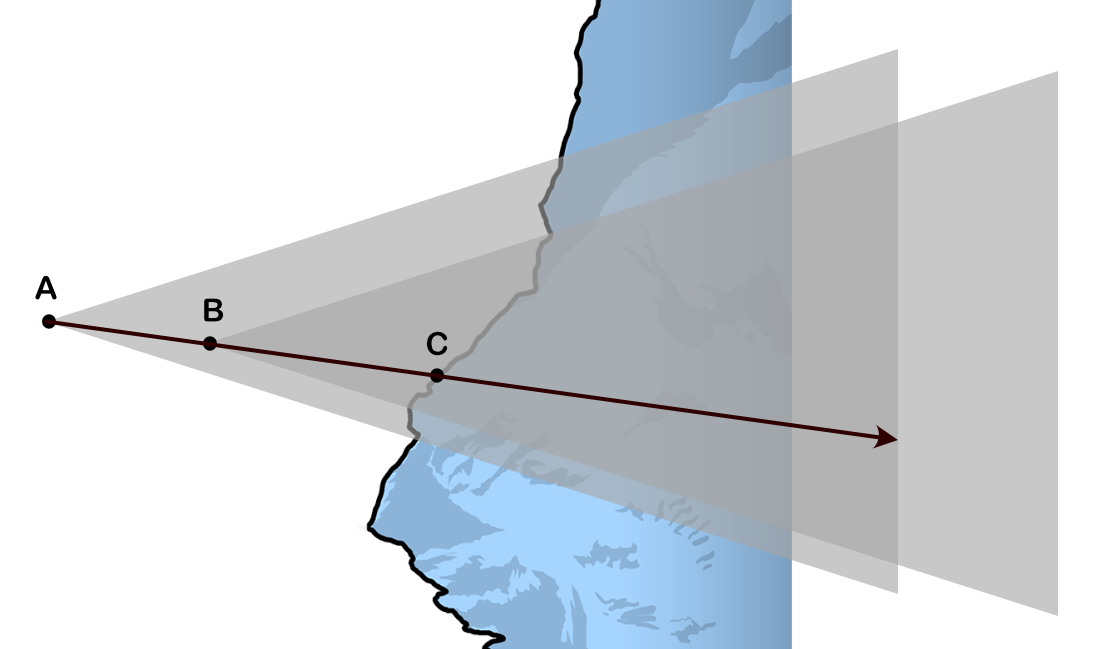
It’s even easier to implement perfect zooming, when you wish to zoom in at the mouse cursor while keeping the scene’s geometry stable at the point. Simply move the camera along the ray that goes from the camera’s position to the cursor’s position. It might also be desirable to adjust the speed of the zoom according to the distance between the camera and the nearest point in the scene that the ray hits. Here’s a diagram just for completeness:

For complete C code implementing the techniques described in this post, look for “map mode” in par_camera_control.h, one of my single-file libraries on GitHub.